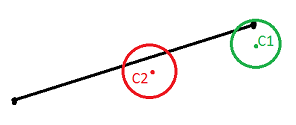
In the first part of the tutorial it was demonstrated how to perform selection of line segments (strokes) by clicking in proximity of the segment ends. Obvious disadvantage of the method is that you cannot perform the selection when the click is done in proximity to the line segment but far from both of its ends. The below figure demonstrates such a case:

According the previous tutorial, click point \(C_1\) will trigger the selection while point \(C_2\) will not. This tutorial will demonstrate how to solve this problem by finding the shortest distance between a clicked point on the screen and a line segment in 3D world.
For simplicity we will keep the same notation for our line segment and denote its end points as \(X_1\) and \(X_2\). Keep in mind: those coordinates are in 3D global system.
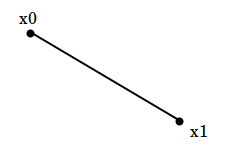
We want to calculate if the mouse ray is close enough (under some threshold) to a line segment \(X_1X_2\). I have already demonstrated how to extract mouse ray parameters from mouse screen coordinates at the ray casting tutorial. From there, we assume we are given mouse ray global 3D coordinates which were called as far and near points. We denote them as \(R_1\) and \(R_2\).
Our task is to extract shortest distance between \(R_1R_2\) and \(X_1X2\). Since the two line segments lie in two different planes (most probably they do), then the shortest distance between segment \(R\) and segment \(X\) is the same as shortest distance between two skew lines.
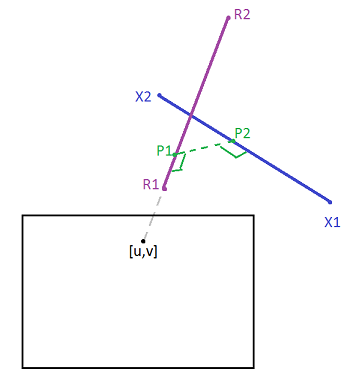
Let’s denote the distance we want to find as \(d\). For given line segments \(r\) and \(x\), we want to find the shortest distance \(d\) between those skew line segments.
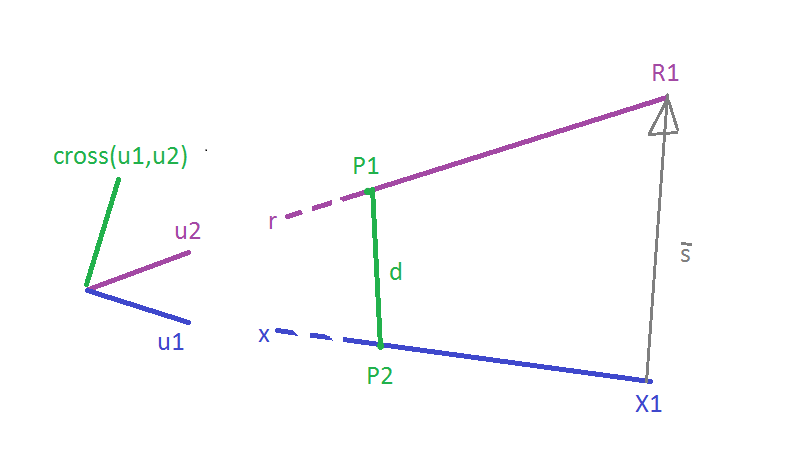
Let \(\vec{s}=R_1-X_1\) is the direction vector from \(R_1\) to \(X_1\). Let \(\vec{u_1}\) and \(\vec{u_2}\) be unit direction vectors for the given line segments. Then we can obtain an orthogonal to both \(x\) and \(r\): it can be found by cross product - \(u_1 \times u_2\). Finally, to obtain scalar \(d\), we need to project \(\vec{s}\) onto \(u_1 \times u_2\), and that can be done by using dot product.
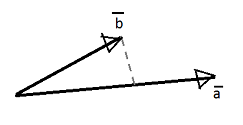
To recap, the scalar projection of vector \(\vec{b}\) onto \(\vec{a}\) is \(\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}|}\).
Therefore, our distance \(d\) is calculated by the next formula: \[d = \dfrac{\vec{s} \cdot (\vec{u_1} \times \vec{u_2})}{| \vec{u_1} \times \vec{u_2} |}\]
Note: we assume the skew lines are not parallel, i.e., \(\vec{u_1} \times \vec{u_2} \neq 0 \).
We only need to change few lines from the first-part line segments intersector. At first, we introduce a method for estimation of \(d\) when given two line segments.
double getSkewLinesDistance(const osg::Vec3d &r1, const osg::Vec3d &r2, const osg::Vec3d &x1, const osg::Vec3d &x2)
{
osg::Vec3d u1 = r2-r1;
osg::Vec3d u2 = x2-x1;
osg::Vec3d u3 = u1^u2;
osg::Vec3d s = r1 - x2;
if (u3.length() == 0)
return 1; // number bigger than threshold, or you could put -1
return std::fabs((s*u3)/u3.length());
}Note: the operator * denotes dot product and operator ^ denotes cross product (OSG syntax).
Now inside the StrokeIntersector::intersect() method that we re-defined in the previous tutorial, we have to change the loop part, leaving all the rest the same:
entity::Stroke* geometry = dynamic_cast<entity::Stroke*>(drawable->asGeometry());
if (geometry)
{
osg::Vec3Array* vertices = dynamic_cast<osg::Vec3Array*>(geometry->getVertexArray());
if (!vertices) return;
// we change the range of the loop since for each iteration
// we need two vertices to pass as parameters for the line segment
for (unsigned int i=1; i<vertices->size(); ++i)
{
// estimate the distance
// s and e variables are estimated earlier and they are mouse ray line segment in 3D
double distance = getSkewLinesDistance(s,e,(*vertices)[i], (*vertices)[i-1]);
// the rest of code remains the same
if (m_offset<distance) continue;
Intersection hit;
// ...
insertIntersection(hit);
}
}This amendment to the earlier tutorial brings the selection of a line stroke to completion.
Check a bit more complex example - OSG intersectors where three different intersectors are presented: line, point and with a virtual plane (based on raycast algortihm). With OSG intersectors code, the fully functional line intersector is used when performing hovering over the wire in order to select it.