Problem overview

Let’s assume we are dealing with a set of values which range wraps around, for example, angles where each angle \( \phi_i \in [0^\circ, 360^\circ) \). The problem occurs when we want to take an average value of such set. To clarify, for given two angles \( \phi_1=1^\circ \) and \( \phi_2=359^\circ \), the angular average is \( 0^\circ \) while the mathematical average is \( \phi_{avg} = \frac{\phi_1+\phi_2}{2} = \frac{1^\circ+359^\circ}{2}=180^\circ \).

In practice, I encoutered this problem while solving a calibration problem of a Time-of-Flight devicei when it was necessary to extract an average phase value from the measured phases of each sensor pixel. When the ToF device was placed at the limit range, the average seemed to be entirely wrong (mathematical average), so we had to come up with a proper formula for the angular average instead.

In this tuturial the formula will be derived, and a C++11-based code snippet will be provided.

Angular average fomula derivation

The solution principle lies in representation of each angle as a vector as it was a radius on a unit circle with the location defined by its angle. See sub-figure a below.

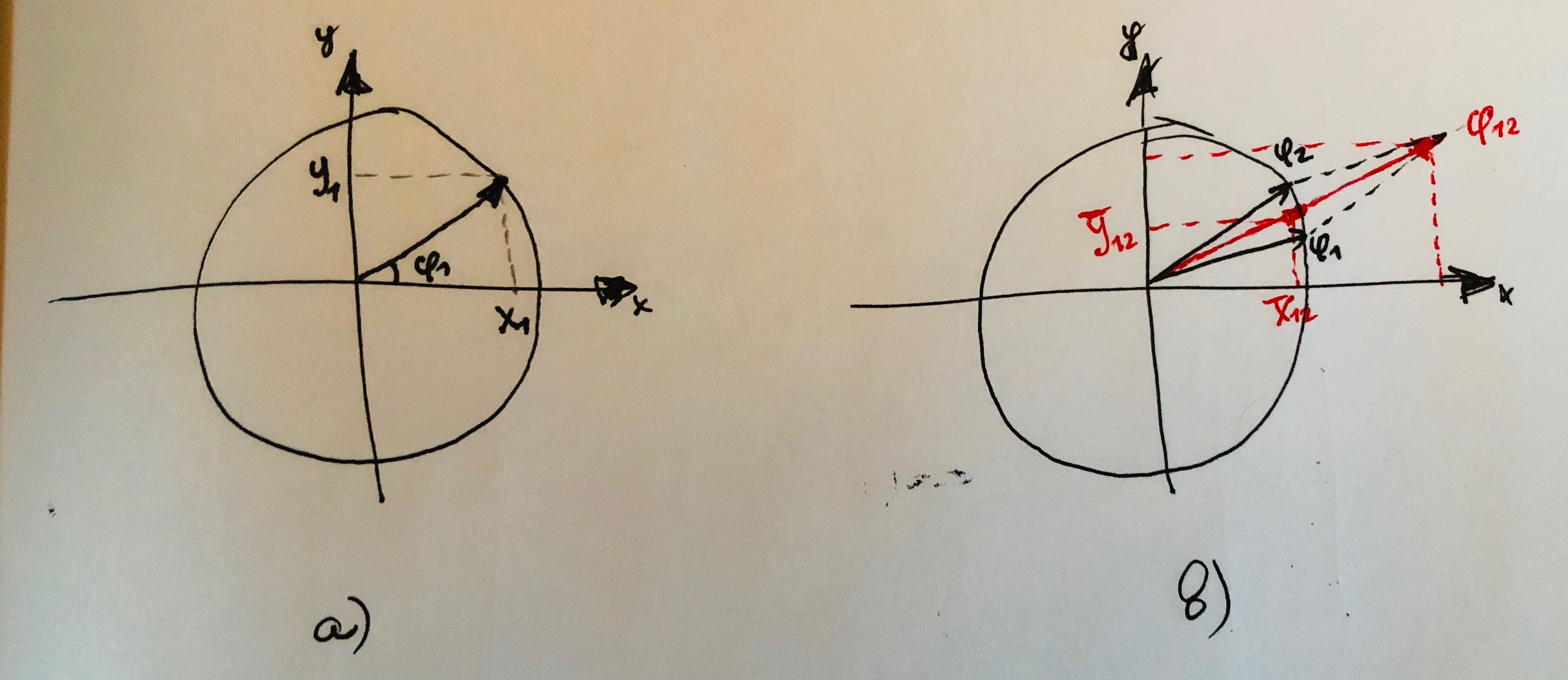
The vector which is defined by the angle \( \phi_1 \) has projections on \(x\) and \(y\) axises. Since the vector forms a right triangle with the \(x\) axis, we can derive the projection values as:

\[ X_i = \cos\phi_i \] \[ Y_i = \sin\phi_i \]

Now, if given a second angle \(\phi_2\) which is represented as a vector (see sub-figure b above), we can use the vector representation in order to calculate the angular average. A simple vector summation will result is a vector with angle \(\phi_{12}\) which will be the average between the two angles as it can be seen on the sub-figure b.

\[X_{\sum} = \sum X_i \] \[Y_{\sum} = \sum Y_i \]

After the “average” vector is obtained, we can use its normalized projection values \(\tilde{X} = normalize(X_{\sum})\) and \(\tilde{Y} = normalize(Y_{\sum})\) in order to extract the angular average using tangent formula:

\[\phi_{avg} = \tan^{-1}(\frac{\tilde{Y}}{\tilde{X}}) \]

Code snippet

The following snippied requires C++11 support:

std::vector<float> X(N);
std::vector<float> Y(N);
std::vector<float> avgAlpha(N);
// vector<float> alpha = ...;
// X = sum(cos(alpha)), Y = sum(sin(alpha))
std::transform(alpha.begin(), alpha.end(), X.begin(), X.begin(),
    [](float alpha, float x0) -> float 
    {
        float xi = std::cos(alpha);
        return xi + x0; 
    } );
std::transform(alpha.begin(), alpha.end(), Y.begin(), Y.begin(),
    [](float p, float y0) -> float 
    {
        float yi = std::sin(alpha);
        return yi + y0; 
    } );
// normalize(x), normalize(y)
// alpha = atan2(y,x)
std::transform(X.begin(), X.end(), Y.begin(), avgPhase.begin(),
    [](float xi, float yi) -> float 
    {
        float length = std::sqrt(xi*xi + yi*yi);
        float unitX = xi/length;
        float unitY = yi/length;
        float alpha = std::atan2(unitY, unitX);
        return alpha<0? alpha+2*M_PI : alpha;
    } );